Reconsidere el problema del flujo de costo mínimo formulado en el problema 9.6.2
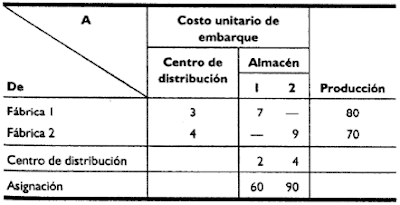
Una empresa fabricará el mismo producto nuevo en dos plantas y después lo mandará a dos almacenes. La fabrica 1 puede enviar una cantidad ilimitada por ferrocarril solo al almacén 1 mientras que la fábrica 2 puede mandar una cantidad ilimitada por ferrocarril solo al almacén 2. Sin embargo, se pueden usar camiones de carga independientes para enviar hasta 50 unidades a cada almacén. En la siguiente tabla se muestra el costo unitario de embarque para cada alternativa junto con las cantidades que se producirán en las fábricas y las cantidades que se necesitan en los almacenes.
A) Obtenga una solución BF inicial resolviendo el árbol de expansión factible que corresponde a usar solo las dos vías y la fabrica 1 que demanda unidades al almacén a través del centro de distribución.
A = Fábrica 1
B = Fábrica 2
C = Centro de distribución
D = Almacén1
E = Almacén2
Maximizar
Z=7XAD+3XAC+4XCE+9XBE+4XBC+2XCD
S. A.
XAD + XAC = 80
XBE = 70
-XAC + XCE = 0
-XAD = -60
-XCE – XBE = -90
Solución:
De ecuación 4 tenemos
-XAD = -60
XAD = 60
Reemplazando en la ecuación 1
XAD + XAC = 80
60 + XAC = 80
XAC = 20
Reemplazando en la ecuación 3
-XAC + XCE = 0
-20 + XCE = 0
XCE = 20
Y de ecuación 2 tenemos que
XBE = 70
Con lo cual, obtenemos una solución BF inicial resolviendo el árbol de expansión factible que corresponde a usar sólo las dos vías y la fábrica 1 que envía unidades al almacén 2 a través del centro de distribución.
B) Use el método simplex de redes (sin usar la rutina de la computadora) para resolver este problema.
Para la solución final hacemos el planteamiento y resolvemos obteniendo el siguiente diagrama, para hallar Z, resolvemos:
Z = 7XAD + 3XAC + 4XCE + 9XBE + 4XBC + 2XCD
Z = 7(30) + 3(50) + 4(50) + 9(40) + 4(30) + 2(30)
Z = 1100